
Verification is the process of determining whether a computational model and its implementation produce predictions with sufficient accuracy, in other words, whether the difference (the error) between the exact (unavailable) and approximate solutions of the model is sufficiently small. Validation is the process of determining the accuracy by which a mathematical model can predict physical events with respect to a decision that has to be made. It addresses the question “Are we solving the right equations?"
Several validation processes have been proposed in the literature. The validation process that will be further studied at the Center is based on a Bayesian inference procedure first introduced in [1,2]. A schematic version of it is described in the figure below. This is the only process, to our best knowledge, that addresses right on the assessment of a model with respect to the QoI on the prediction scenario. This is extremely important as it recognizes that a model may be valid for the prediction of one QoI but invalid for a different QoI.
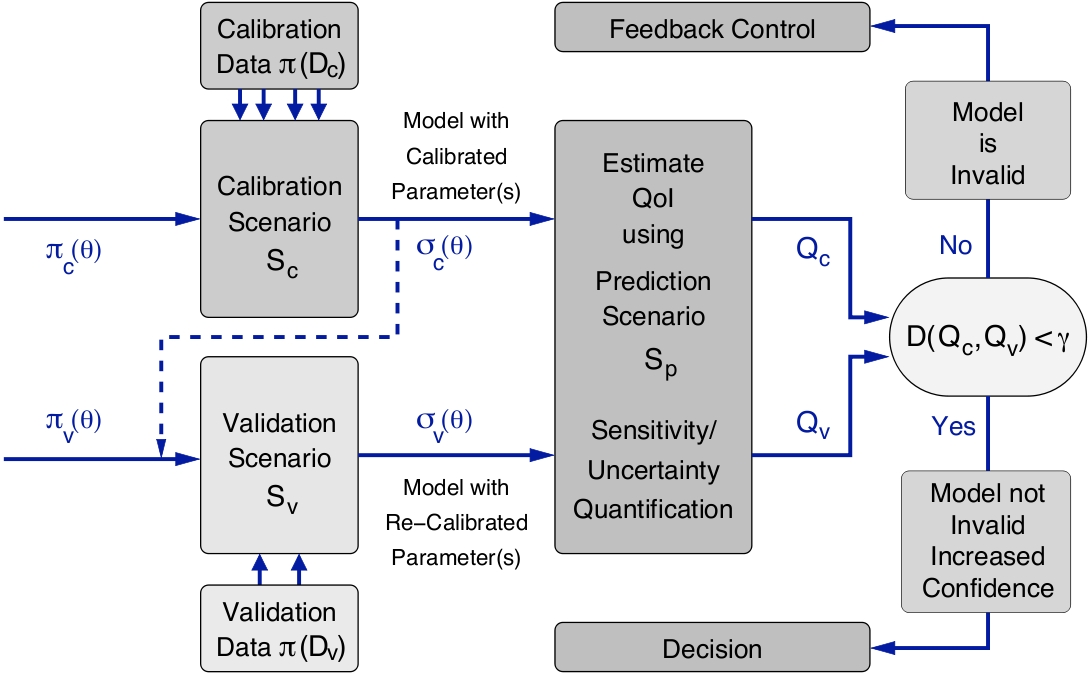
Flowchart of the validation process
Thrust Leaders: Serge Prudhomme and Raul Tempone