Uncertainty Quantification is the process by which uncertainties in a system are characterized and propagated to a given Quantity of Interest (QoI). The characterization of uncertainties relates in general to the solution of so-called inverse problems while uncertainty propagation is often associated with the solution of forward problems. An additional goal of UQ is to reduce uncertainties in the QoI based on the collection of new data or on better physical understanding. Performing UQ for complex applications is a daunting task. This is mainly due to the fact that UQ is computationally challenging and that data, obtained either from experiments, legacy data sets, literature, or from expert opinion, are often scarce, incomplete, and even contradictory.
In order to overcome these challenges, the participants of the UQ Center and their collaborators will cover distinct components of fundamental knowledge such as:
a) Numerical Solution of Stochastic Differential Equations
b) Numerical Optimization
c) Reduced Order Modeling
d) Inverse Problems
e) Multiscale methods
f) Multiphysics
g) Sensitivity Analysis
h) Automatic Differentiation
i) Adjoint based methods for control, discretization and model error estimation, and Uncertainty Quantification,
j) Bayesian Statistics
k) Functional Data Analysis, and
l) Compressive Sensing.
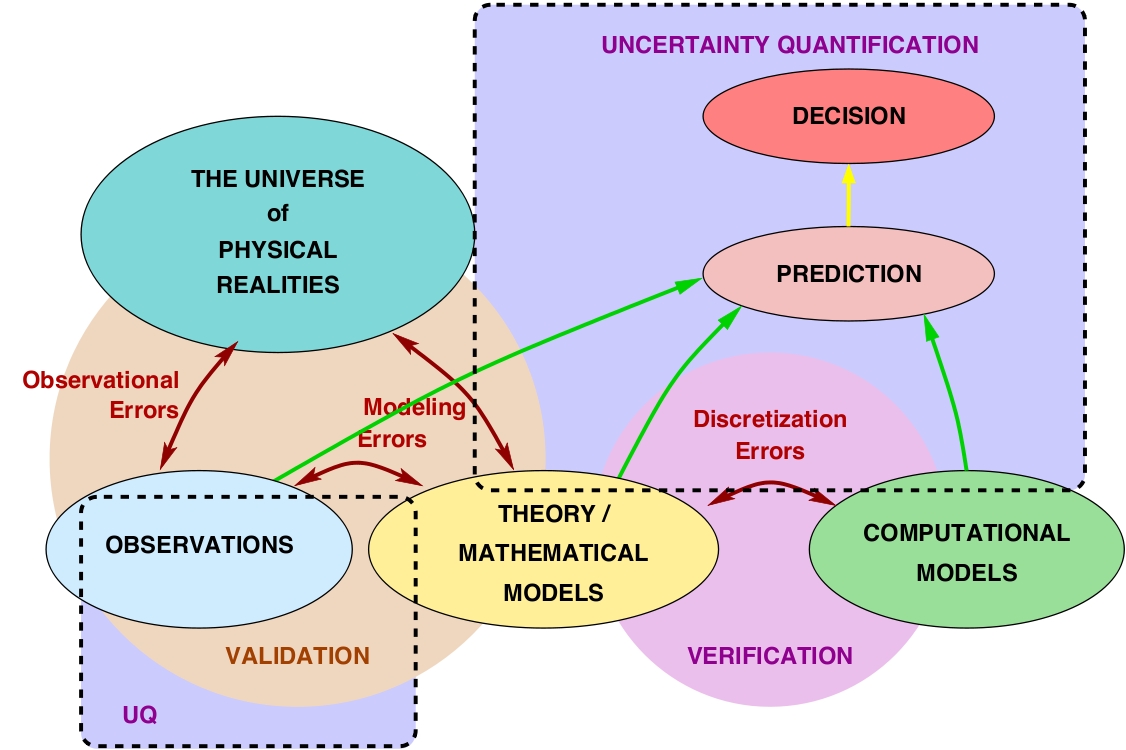
Conceptual Diagram for Uncertainty Quantification and Verification & Validation
Thrust Leaders: Raul Tempone and Omar Knio

